函数的单调性

　　一般地，设一连续函数 f(x) 的定义域为D，则

　　如果对于属于定义域D内某个区间上的任意两个自变量的值x1，x2∈D且x1>x2，都有f(x1) >f(x2)，即在D上具有单调性且单调增加，那么就说f(x) 在这个区间上是增函数。

　　相反地，如果对于属于定义域D内某个区间上的任意两个自变量的值x1，x2∈D且x1>x2，都有f(x1)

　　则增函数和减函数统称单调函数。

　　函数单调性的几何特征：在单调区间上，增函数的图象是上升的，减函数的图象是下降的。

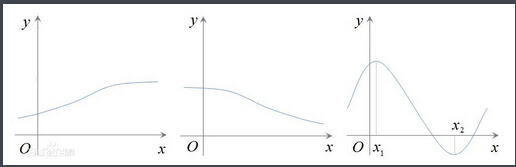
　　当x1 < x2时，都有f(x1)<f(x2)

　　当x1 < x2时，都有f(x1)>f(x2) 。

　　如上图右所示，对于该特殊函数f(x)，我们不说它是增函数或减函数，但我们可以说它在区间 [x1，x2]上具有单调性。