直线y=-43x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,求直线AM的解析式.
题型:不详难度:来源:
| 4 |
| 3 |

答案
∴点A的坐标为:(6,0),点B坐标为:(0,8),
∵∠AOB=90°,
∴AB=
| OA2+OB2 |
由折叠的性质,得:AB=AB′=10,
∴OB′=AB′-OA=10-6=4,
设MO=x,则MB=MB′=8-x,
在Rt△OMB′中,OM2+OB′2=B′M2,
即x2+42=(8-x)2,
解得:x=3,
∴M(0,3),
设直线AM的解析式为y=kx+b,代入A(6,0),M(0,3)得:
|
解得:
|
∴直线AM的解析式为:y=-
| 1 |
| 2 |
举一反三
| A.两个全等的三角形一定关于某条直线对称 |
| B.直角三角形是轴对称图形 |
| C.关于某条直线对称的两个三角形一定全等 |
| D.锐角三角形都是轴对称图形 |
 AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为______.
AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为______.(1)请你在x轴上找一点C,使它到点A、B的距离之和为最小,则点C的坐标为(______,______);
(2)在图中,作出△ABC关于直线y轴的对称图形△A′B′C′;
(3)直接写出△A′B′C′三个顶点坐标.


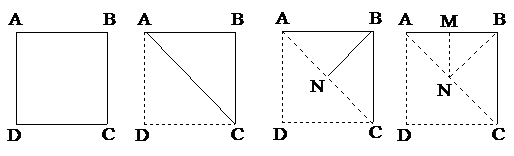
| A.四个相同的正方形 |
| B.一个等腰直角三角形和一个正方形 |
| C.多个等腰直角三角形 |
| D.两个相同的正方形 |
最新试题
- 发源于西欧的启蒙运动能迅速波及欧洲大多数国家的主要原因是 A.法国启蒙思想家到欧洲各地处发表反封
- (满分13分)已知且(1)求的表达式;(2)判断的奇偶性与单调性,并给出必要的说明;(3)当的定义域为时,如果恒成立,
- China is ___ the east of Asia while Japan is ___ the east of
- 日常生活中的下列做法,正确运用了化学知识的是:①用汽油洗除衣服上的油污②用砂纸打磨掉铝制品表面的“污渍”③加少量亚硝酸盐
- (x﹣1)(x+2)=2(x+2)的根是( ).
- 互联网不仅整合了其他媒体的优点,还有自己独特的优势。它使每个网民参与到信息传递过程中,使读者有机会成为作者,使观众有机会
- 读下列锋面示意图,回答问题。(1)甲、乙两图中属于冷气团的是_______,属于暖气团的是_______。(2)影响我国
- 下列各句没有通假字的一项是( )A.召有司案图B.唯大王与群臣孰计议之 C.畔主背亲D.汉亦留之以相当
- 设函数f(x)=6-x2(x≤6)x2+x-2(x>6)
- 解含未知数x的分式方程:(1)32x-2+11-x=3(2)4x+1+5x-1=10x2-1
热门考点
- The film Harry Potter Ⅳ is _______ for children above 12 and
- 根据句意及首字母写出单词。1. Jean sends me a p__________. 2. Do you know
- 填空。(1)孟子,名_______,字子舆,是________之后的_________大师。战国时期著名的_______
- It was ______ the second-hand bus that the mechanic spent th
- 【题文】不等式的解集为,则函数的零点为A.和B.C.D.和2
- Monday,Scott comes to school at 8:15 in the morning. He ha
- 阅读下面这首诗,然后回答问题。墨梅①王冕我家洗砚池②头树,朵朵花开淡墨痕。不要人夸颜色好,只留清气满乾坤。【注】①墨梅:
- 补写下列名句名篇中的空缺部分(4分,任选两题)(1) , ,不知老之将至。(《论语·述而
- 用“*”定义一种新运算:对于任意有理数a,b,都有a*b=ab-a2,例如,2*3=2×3-22=2,那么2*(-12)
- 中世纪西欧封建制度产生和基本确立的时间大体为( )A.6世纪上半叶和11世纪前后B.6世纪下半叶和11世纪前后C.6世纪
© 2017-2019 超级试练试题库,All Rights Reserved.