抛物线的定义与方程
抛物线的定义
抛物线定义：平面内与一个定点F 和一条直线l 的距离相等的点的轨迹叫做抛物线，点F 叫做抛物线的焦点，直线l 叫做抛物线的准线，定点F不在定直线上。它与椭圆、双曲线的第二定义相仿，仅比值(离心率e)不同，当e=1时为抛物线，当0<e<1时为椭圆，当e>1时为双曲线。
抛物线的方程
抛物线的标准方程有四种形式，参数p的几何意义，是焦点到准线的距离，掌握不同形式方程的几何性质(如下表)：其中P(x0,y0)为抛物线上任一点。
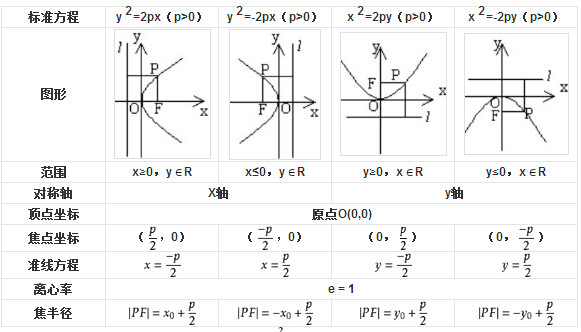
对于抛物线y2=2px(p≠0)上的点的坐标可设为(
,y0)，以简化运算。抛物线的焦点弦：设过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A(x1，y1)、B(x2，y2)，直线OA与OB的斜率分别为k1,k2，直线l的倾斜角为α，则有y1y2=-p2，x1x2=
，k1k2=-4，|OA|=
,|OB|=
,|AB|=x1+x2+p
相关试题
如图，在正方体ABCD-A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是 
[ ]
A．直线
B．双曲线
C．抛物线
D．圆抛物线P：x2=2py上一点Q（m，2）到抛物线P的焦点的距离为3，A、B、C、D为抛物线的四个不同的点，其中A、D关于y轴对称，D（x0，y0）， B（x1，y1）， C（x2，y2），-x0＜x1＜x0＜x2，直线BC平行于抛物线P的以D为切点的切线。
（1）求p的值；
（2）证明：∠BAC的角平分线在直线AD上；
（3）如果点D到直线AB、AC的距离分别为m、n，且m+n=
|AD|，△ABC的面积为48，求直线BC的方程。设抛物线C：y2=2px(p＞0)的焦点为F，其准线与x轴的交点为Q，过点F作直线交抛物线C于A、B两点，若∠QBF=90°，则|AF|-|BF|=（ ）。 如图，在正方体ABCD-A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是 
[ ]
A．直线
B．圆
C．双曲线
D．抛物线已知F是抛物线C：y2=4x的焦点，过F且斜率为1的直线交C于A，B两点．设|FA|＞|FB|，则|FA|与|FB|的比值等于（ ）。 已知F为抛物线y2=3x的焦点，P为抛物线上任一点，A（3，2）为平面上一定点，则|PF|+|PA|的最小值为（ ）。 如图，在正方体ABCD﹣A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是 
[ ] A．直线
B．圆
C．双曲线
D．抛物线抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4，则点M的横坐标x=______． 直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线交于A、B两点，若线段AB的长是8，AB的中点到y轴的距离是2，则此抛物线方程是（ ） A．y2=12x B．y2=8x C．y2=6x D．y2=4x 已知抛物线y2=4x的焦点为F，准线与x轴的交点为M，N为抛物线上的一点，且|NF|=
|MN|，则∠NMF=（ ）3 2 A． π 6 B． π 4 C． π 3 D． 5π 12 抛物线x=
y2的焦点坐标为（ ）1 4a A．(
，0)1 16a B．（a，0） C．(0，
)1 16a D．（0，a） 若抛物线y2=4x上一点P到其焦点的距离为3，则点P的横坐标等于______． 过抛物线y2=4x的焦点作直线l交抛物线于A、B两点，若线段AB中点的横坐标为3，则|AB|等于（ ） A．2 B．4 C．6 D．8 有一矩形纸片ABCD，按图所示方法进行任意折叠，使每次折叠后点B都落在边AD上，将B的落点记为B′，其中EF为折痕，点F也可落在边CD上，过B′作B′H∥CD交EF于点H，则点H的轨迹为（ ） A．圆的一部分 B．椭圆的一部分 C．双曲线的一部分 D．抛物线的一部分 
已知曲线C上的动点P（x，y）满足到点F（0，1）的距离比到直线l：y=-2的距离小1．
（Ⅰ）求曲线C的方程；
（Ⅱ）动点E在直线l上，过点E分别作曲线C的切线EA，EB，切点为A、B．
（ⅰ）求证：直线AB恒过一定点，并求出该定点的坐标；
（ⅱ）在直线l上是否存在一点E，使得△ABM为等边三角形（M点也在直线l上）？若存在，求出点E坐标，若不存在，请说明理由．如图，正方体ABCD-A1B1C1D1的棱长为3，点M在AB上，且AM=
AB，点P在平面ABCD上，且动点P到直线A1D1的距离与P到点M的距离相等，在平面直角坐标系xAy中，动点P的轨迹方程是______．1 3 
设抛物线y2=8x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．如果直线AF的斜率为-
，那么|PF|=（ ）3 A．4 3 B．8 C．8 3 D．16 若点A的坐标为（3，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为（ ） A．（0，0） B．(
，1)1 2 C．(1，
)2 D．（2，2） 设抛物线x2=12y的焦点为F，经过点P（2，1）的直线l与抛物线相交于A、B两点，若点P恰为线段AB的中点，则|AF|+|BF|=______． 设抛物线y2=8x上一点P到y轴的距离是4，则点P到该抛物线焦点的距离是（ ） A．4 B．6 C．8 D．12 若圆C过点M（0，1）且与直线l：y=-1相切，设圆心C的轨迹为曲线E，A、B为曲线E上的两点，点P(0，t)(t＞0)，且满足
=λAP
(λ＞1)．PB
（I）求曲线E的方程；
（II）若t=6，直线AB的斜率为
，过A、B两点的圆N与抛物线在点A处共同的切线，求圆N的方程；1 2
（III）分别过A、B作曲线E的切线，两条切线交于点Q，若点Q恰好在直线l上，求证：t与
•QA
均为定值．QB 已知点P是长方体ABCD-A1B1C1D1底面ABCD内一动点，其中AA1=AB=1，AD=
，若A1P与A1C所成的角为30°，那么点P在底面的轨迹为（ ）2 A．圆弧 B．椭圆的一部分 C．双曲线的一部分 D．抛物线的一部分 动点P到直线x+2=0的距离减去它到M（1，0）的距离之差等于1，则动点P的轨迹是______． 若点P到直线x=-1的距离比它到点（2，0）的距离小1，则点P的轨迹为（ ） A．圆 B．椭圆 C．双曲线 D．抛物线 已知F为抛物线y2=2px（p＞0）的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点，|PA|+|PF|最小值为8．
（1）求该抛物线的方程；
（2）若直线x-y-3=0与抛物线交于B、C两点，求△BFC的面积．直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线交于A、B两点，若线段AB的长是8，AB的中点到y轴的距离是2，则此抛物线方程是（ ） A．y2=12x B．y2=8x C．y2=6x D．y2=4x 抛物线y2=4x上的点M到其焦点F的距离为4，则点M的横坐标是______． 一个动圆的圆心在抛物线y2=8x上，且动圆恒与直线x+2=0相切，则动圆必过定点（ ） A．（0，2） B．（0，-2） C．（2，0） D．（4，0） 已知抛物线y2=2x的焦点是F，点P是抛物线上的动点，又有点A（3，2），则|PA|+|PF|取最小值时P点的坐标为______． 若点P到直线y=-1的距离比它到点（0，3）的距离小2，则点P的轨迹方程为 （ ） A．x2=12y B．y2=12x C．x2=4y D．x2=6y 平面上动点M到定点F（3，0）的距离比M到直线l：x+1=0的距离大2，求动点M满足的方程． 到定点（2，1）和定直线x+2y-4=0的距离相等的点的轨迹是______． 动点P到定点A（0，-2）的距离比到定直线l：y=10的距离小8，则动点P的轨迹为______． 一动圆圆心在抛物线x2=4y上，过点（0，1）且与定直线l相切，则l的方程为（ ） A．x=1 B．x= 1 16 C．y=-1 D．y=- 1 16 抛物线y=4x2上的一点M到焦点的距离为1，则点M的纵坐标是______． 设抛物线y2=2px（p＞0）的焦点为F，点A（0，2）．若线段FA的中点B在抛物线上，则B到该抛物线准线的距离为______． 已知动圆M经过点A（3，0），且与直线l：x=-3相切，求动圆圆心M的轨迹方程． 已知F是抛物线y2=x的焦点，A、B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到y轴的距离为______． 设抛物线y2=4x上一点P到直线x=-3的距离为5，则点P到该抛物线焦点的距离是（ ） A．3 B．4 C．6 D．8 动点到点（3，0）的距离比它到直线x=-2的距离大1，则动点的轨迹是（ ） A．椭圆 B．双曲线 C．双曲线的一支 D．抛物线 已知抛物线y2=4x的焦点为F，准线与x轴的交点为M，N为抛物线上的一点，且|NF|=
|MN|，则∠NMF=（ ）3 2 A． π 6 B． π 4 C． π 3 D． 5π 12 已知两点M（-2，0）、N（2，0），点P为坐标平面内的动点，满足|
|•|MN
|+MP
•MN
=0，则动点P（x，y）的轨迹方程为（ ）NP A．y2=8x B．y2=-8x C．y2=4x D．y2=-4x 抛物线y2=4x上一点P到焦点F的距离是10，则P点的坐标是（ ） A．（9，6） B．（6，9） C．（±6，9） D．（9，±6） 若点P到点F（4，0）的距离比它到直线x+5=0 的距离小1，则P点的轨迹方程是（ ） A．y2=-16x B．y2=-32x C．y2=16x D．y2=32x 抛物线y=ax2的准线方程是y=2，则a的值为（ ） A． 1 8 B．- 1 8 C．8 D．-8 已知动圆C过定点F（1，0），且与定直线x=-1相切．
（Ⅰ） 求动圆圆心C的轨迹T的方程；
（Ⅱ）若轨迹T上有两个定点A、B分别在其对称轴的上、下两侧，且|FA|=2，|FB|=5，在轨迹T位于A、B两点间的曲线段上求一点P，使P到直线AB的距离最大，并求距离的最大值．
，常数a>0，定义运算“*”：
，若
，则动点
的轨迹是 
最新试题
- 已知，延长BC到D，使．取的中点，连结交于点．(1). （5分）求的值；(2). （3分）若，求的长．
- 如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别为线段DD1，BD的中点．（1）求异面直线EF与BC
- 如图，展示的某人正在湖面上划独木舟的画面，请你观察图片，想象人划独木舟的情景，提出两个物理问题．如
- 下列有关物质的量浓度关系正确的是 A．物质的量浓度相等CH3COOH和CH3COONa溶液等体积混合，溶
- 某原子结构示意图为，它的核电荷数和最外层电子数分别是（ ）A．6和8B．8和6C．8和2D．6和2
- 假设你是学生李华，近日你班同学参加了世界自然基金会WWF组办的“我为哥本哈根减斤碳”活动，大家开始在日常生活中减少能源、
- The world is filled with smart, talented, educated and gifte
- 将标号为1，2，3，4，5，6的6个小球放入3个不同的盒子中．若每个盒子放2个，其中标号为1，2的小球放入同一盒子中，则
- 公元前260年，秦大破东方六国中实力最强的赵国军队，坑***赵军士卒40多万人，从此，六国再也无力抵御秦国攻势。这场战争是
- I"d like to buy a necklace to____________ my new dress.[
热门考点
- 阅读下面的文字，完成3题《陈书》目录序 曾巩《陈书》六本纪，三十列传，凡三十六篇，唐散骑常侍姚思廉撰。始思廉父察，梁、陈
- 2003年5月13日，安徽淮北芦岭煤矿发生特大瓦斯爆炸事故，造成86人死亡、28人受伤．此前，贵州木冲沟煤矿、山西孟南庄
- 阅读短文内容，根据已给的首字母填入短文所缺的单词。 Will it matter if you don"t ha
- 如图，表示在空中飞行的足球，质量为420g，画出它所受重力的示意图．
- 12002用科学记数法表示为______．
- 阅读下面短文，从短文后各题的A、B、C、D四个选项中，选取出适合填入空白处的最佳选项，并在答题卡上将该选项涂黑。Ther
- 某校初三学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．下
- 已知在100℃的温度下(本题涉及的溶液其温度均为100℃，水的离子积KW＝1.0×10－12 mol2·L－2。下列说法
- 葡萄糖分子中含有______和______官能团，由于具有______官能团，能发生银镜反应，其化学方程式是______
- 在宏观、微观和符号之间建立联系是化学学科的特点。(1)在水、铜和氯化钠3种物质中，由分子构成的是________。(2)
© 2017-2019 超级试练试题库,All Rights Reserved.